RX-Bayes: Bayesian Reasoning in Practice

Rx-Bayes is a clinical decision support tool that calculates real-time probability adjustments based on test characteristics and pretest probability. It makes Bayesian reasoning explicit, transparent, and reproducible.

The Problem

Clinicians are taught to order tests. Unfortunately, they are not taught to interpret them correctly. Many doctors, especially in functional medicine, have taken their poor understanding and popularized it, teaching their incorrect, but appealingly simple, interpretation to patients.

A positive test does not mean the patient has the disease. A negative test does not mean the patient is healthy. The value of any test depends entirely on the pretest probability — the likelihood of disease before the test is performed.

Most clinicians do not calculate pretest probability. They do not adjust for sensitivity and specificity. They treat test results as binary verdicts rather than probabilistic updates. This leads to overdiagnosis, overtreatment, and unnecessary harm.

This is not speculation. Studies have shown that clinicians perform poorly on tests requiring an understanding of pretest probability and Bayesian reasoning [Stovitz, 2020]. The problem has magnified now that the public is starting to act as their own physicians, interpreting bloodwork and testing based on "training" from podcasters who themselves are amateurs.

Bayesian reasoning is the mathematically correct framework for interpreting medical testing. But Bayesian reasoning is difficult, because it forces us to think of our beliefs as probabilities of certainty, not as binaries of true/false, right/wrong. Worse, the math itself is not intuitive. The calculations are tedious. And the uncertainty ranges (confidence intervals for sensitivity, specificity, and prevalence) compound the complexity.

RX-Bayes was built to assist with this problem, by helping to create a more intuitive understanding of how Bayes' theorem works in real clinical scenarios, and especially how pretest probability has a profound impact on test interpretation. It functions both as both a teaching tool, helping clinicians develop their Bayesian intuition, and as a reference tool for applying Bayesian reasoning to common clinical conditions.

What It Does

RX-Bayes allows clinicians to adjust
three inputs in real-time:

1. Pretest probability – The likelihood of disease before testing, based on clinical presentation, age, and risk factors.
2. Sensitivity – The probability that the test is positive if the disease is present.
3. Specificity – The probability that the test is negative if the disease is absent.

The tool then calculates the information we REALLY want to know:

• Positive predictive value (PPV) – The probability of disease if the test is positive.
• Negative predictive value (NPV) – The probability of disease if the test is negative.

It also allows users to specify uncertainty ranges for each input (e.g., sensitivity 82-86%, specificity 90-98%) and displays the resulting range of possible outcomes.

The tool includes pre-populated data for common conditions: strep throat, pneumonia, pulmonary embolus, UTI, breast cancer, and others. Users can also create custom scenarios and save them for future reference.

A Note on Design From Dr. Z

RX-Bayes was built as a clinical tool, not a marketing asset. I wrote it years ago, without input from any graphic designers. The colors are ... well ... atrocious. But, in the end, it was designed for function, not aesthetics. The interface reflects my background as a practicing clinician, with limited aesthetic capability.

With that said, the main interface is intentionally minimal: three sliders, two outputs, and no distractions. It's intended to invite you to "play around", and see how the numbers change.

How It Works: The Strep Throat Example

Consider a 45-year-old patient with a sore throat. No fever. No exudate. No lymphadenopathy. No cough. The nurse runs a rapid strep test according to protocol.

The test comes back positive.

Does the patient have strep throat?

Most clinicians would say yes. The test is positive. Treat with antibiotics.

But the Bayesian answer is different.

Step 1: Estimate Pretest Probability

A 45-year-old with a sore throat but no other symptoms has a very low pretest probability of strep throat, it's around 1%. Strep is rare in adults, especially without fever, exudate, or lymphadenopathy.

So the pretest probability is 1%.

Step 2: Apply Test Characteristics

The rapid strep test, according to manufacturer specifications using controlled samples has:

• Sensitivity: 84%
• Specificity: 97%

This means in people who we know for sure have strep, the test will catch 84% of them. And in people we know for sure do NOT have strep, the test will correctly identify 97% of them.

Step 3: Calculate Post-Test Probability

Using Bayes' theorem, the post-test probability of strep throat given a positive test is 22%.

Not 84%. Not 95%. 22%.

This means that even with a positive test, there is a 78% chance the patient does not have strep throat. The test is not actionable. Treatment is not indicated. The test probably should not have been ordered in the first place.

How?

If a doctor saw 1000 patients exactly like this, about 10 of them would have Strep Throat, and 990 would not have it.

If your doctor ran tests on all 1000 patients, the following would happen:

10 patients would have the condition (green), and the test would correctly identify 84% of them (~8 true positives, in dark green)

990 patients would not have the condition, and the test would correctly identify 97% of them (~960 true negatives, in grey)

2 patients would have the condition, but the test would BE WRONG, and say that they do not have the condition (false negatives, in light green)

30 patients would NOT have the condition, but the test would BE WRONG, and say that they do have the condition (false positives, in red)

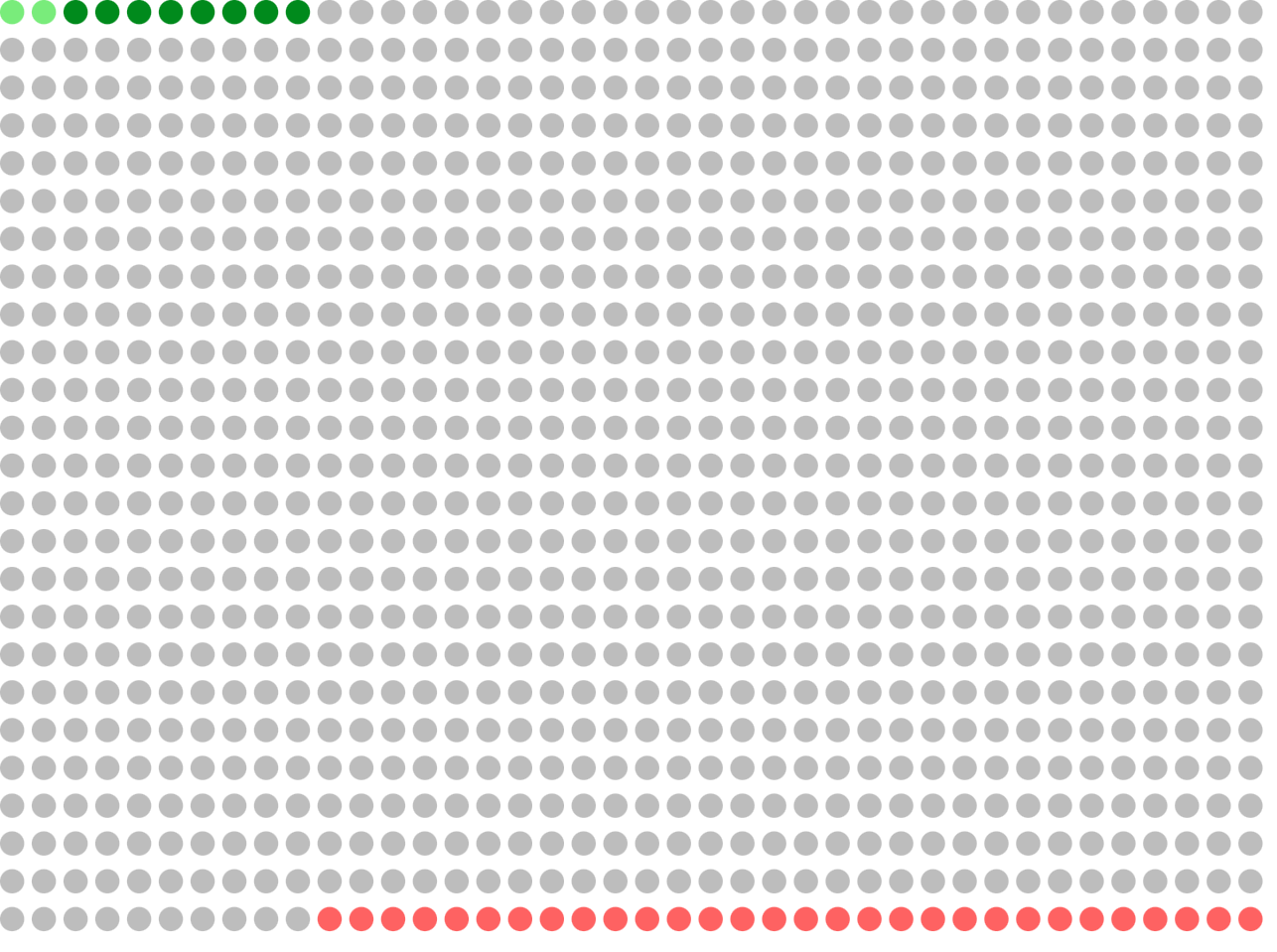
Total: 1000

So, if your test is positive, to figure out what it means, you group all the positive tests together: 8 true positives and 30 false positives, for a total of 38 positive tests.

The chance that your test is a true positive is (8/38), which is ~21%

In the app, the way we show that is a pretest of 1% (10 out of 1000), sensitivity of 84%, and specificity of 97%:

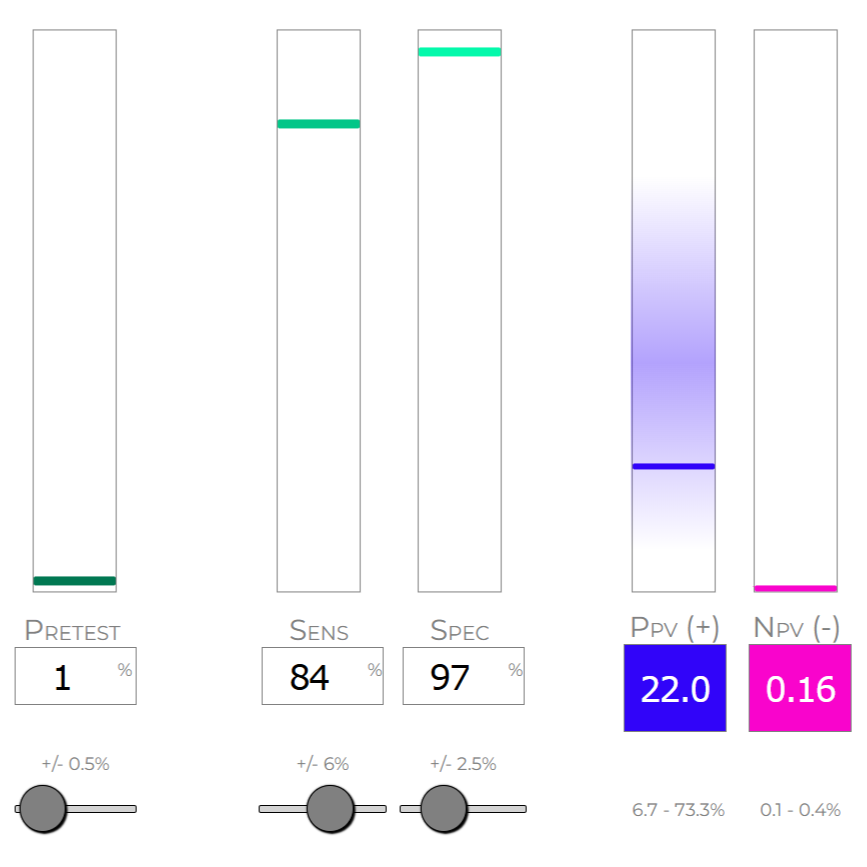
You can see that the app shows that a positive test has only a 22% chance of being a true positive (the app calculates 22% because it's accounting for more decimal places, not rounding as we did here).

Compare to a Different Scenario

Now consider a 5-year-old child with the same positive test result. But this child also has fever, exudate, and lymphadenopathy.

The pretest probability is now ~52%.

If the test is positive, the probability of strep throat is ~97%.

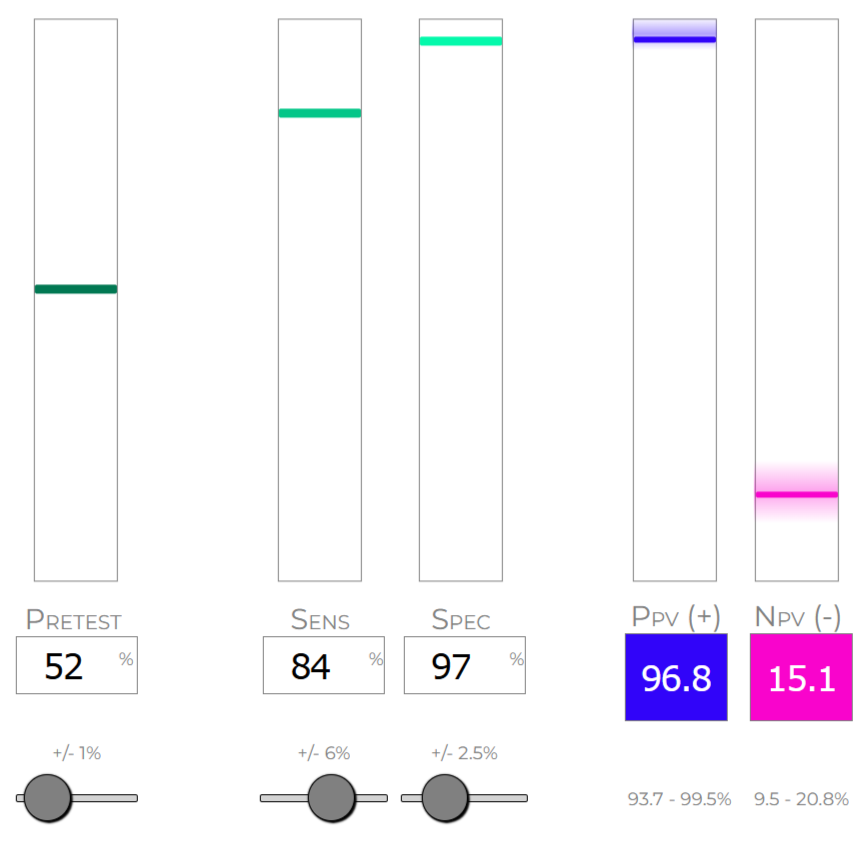
Same test. Different patient. Completely different interpretation.

This is why Bayesian reasoning matters.

Video Walkthrough

Rx-Bayes App Walkthrough Video

Dr. Z provides a complete walkthrough of the tool, demonstrating how to use the sliders, interpret the outputs, and apply Bayesian reasoning to common clinical scenarios.

Access the Tool

Rx-Bayes is publicly accessible at rxbayes.com